Сфе́ра (греч. σφαῖρα — мяч) — замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, называемой центром сферы. Сфера также является телом вращения, образованным при вращении полуокружности вокруг своего диаметра. Сфера является поверхностью шара.
Еще древние греки считали окружность и сферу идеальными формами. Потверждение этому можно наблюдать в природе: многие плоды и ягоды имеют форму шара или близкую к ней, например арбуз, апельсин, смородина. Шаровидная форма используется в технике, например, в подшипниках. Во многих играх снаряд имеет форму шара: мяч в футболе, волейболе, тенесе, гольфе, шар в бильярде и др. Хорошо всем знакомый ёлочный шарик — на самом деле сфера, так как сделан из очень тонкого стекла и внутри пустой.
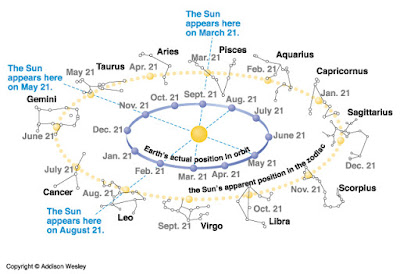
Форму шара имеет наша планета и большинство космических тел. А так как планеты, Солнце, Луна и звёзды движутся по воображаемой «небесной сфере», то естественно, для изучения их движения потребовалось знание геометрии сферы.
При решении задач практического характера и, в первую очередь, задач астрономии возникла сферическая геометрия. Эти задачи были необходимы, например, путешественникам и мореплавателям, которые ориентировались по звёздам.
Сведения о сфере были необходимы и при решении сугубо земных задач — вычислении географических координат, для составления географических карт, для нахождения курса корабля. В настоящее время, существуют различные науки в основе которых лежит сферическая геометрия. Например, математическая картография изучает способы отображения поверхности Земли на плоскости. Поскольку поверхность Земли (приблизительно сферическая) имеет конечную кривизну, её нельзя отобразить на плоскость с сохранением всех пространственных отношений одновременно: углов между направлениями, расстояний и площадей поверхностей. Можно сохранить только некоторые из этих соотношений. Важное понятие в математической картографии — картографическая проекция, то есть функция, задающая отображение географических координат точек на поверхности Земли на декартовы координаты на плоскости. Область картографии — составление и оформление карт.
Первой по времени геометрией, отличной от евклидовой, была сферическая геометрия, или сферика. Сферика возникла позже, чем евклидова геометрия плоскости и пространства. Основными стимулами для возникновения геометрии плоскости и пространства была необходимость измерения площадей полей и других плоских фигур и вместимости сосудов и амбаров различной формы. Основным стимулом для возникновения сферики было изучение звёздного неба.
Древние греки познакомились с вавилонской астрономией по крайней мере в IV в. до н. э., когда первоначальные названия планет были заменены названиями планет по вавилонскому образцу, латинскими переводами которых являются общепринятые нами названия. Астрономия, изложенная в «Альмагесте» Птолемея, была результатом продолжавшегося несколько веков развития науки, впитавшей традиции как вавилонских астрономов, так и греческих геометров.
Сферика Автолика. Первым античным математическим сочинением, сохранившимся до наших дней, является книга «О движущейся сфере» Автолика, жившего в конце IV в. до н. э. Предметом исследования этой книги является небесная сфера, рассматриваемая, однако, в весьма абстрактном виде. Книга Автолика состоит из 12 предложений. Определения относятся к равномерному движению. В предложении 1 доказывается, что если сфера равномерно движется вокруг оси, то все её точки, не лежащие на оси, описывают параллельные круги, имеющие те же полюсы, что и сфера, а плоскости этих кругов перпендикулярны оси сферы. Под кругами здесь понимаются плоские фигуры, ограниченные окружностями, а под выражением «точка описывает круг» понимается то, что точка пробегает окружность круга.
Сферика Феодосия. Первое дошедшее до нас систематическое изложение сферической геометрии содержится в «Сферике» Феодосия, жившего во II-I вв. до н. э. «Сферика» Феодосия состоит из трёх книг, в первой из которых шесть определений и 23 предложения, во второй – одно определение и 23 предложения, в третьей – 14 предложений. Определение Феодосия: «Сфера есть телесная фигура, содержащая внутри одной поверхности, такая, что все прямые, падающие на неё из одной точки внутри фигуры, равны между собой». Большинство предложений «Сферики» Феодосия – стереометрические теоремы и задачи на построение.
Сферика Менелая. Значительно более развитую сферическую геометрию можно найти в трактате «О сфере» Менелая, жившего в конце I в. н. э. Сочинение Менелая сохранилось только в арабском переводе в нескольких обработках, лучшими из которых являются обработки Абу Насра ибн Ирака и Насир ад-Дина ат-Туси. «Сферика Менелая состоит из трёх книг, содержащих соответственно 39, 21 и 25 предложений. Во введении к книге I Менелай даёт определение сферического треугольника («трёхсторонней фигуры»), т.е. части поверхности, ограниченной тремя дугами больших кругов, меньшими полукругами, и углов сферического треугольника. Если большинство предложений «Сферики» Феодосия были стереометрическими, сочинение Менелая посвящено геометрии на поверхности сферы, трактуемой по аналогии с планиметрией Евклида.
Сфера, большая и малая окружности
Сферой называется геометрическое место точек пространства, расположенных на данном расстоянии от данной точки, называемой её центром. Отрезок, соединяющий центр сферы с какой-либо его точкой, называется радиусом сферы. Отрезок, соединяющий де точки сферы и проходящий, кроме того, через его центр, называется диаметром. Из определения следует, что все радиусы равны и что диаметр равен удвоенному радиусу. Плоскость, проходящая через центр сферы, называется диаметральной плоскостью.
Так как через всякие три точки пространства, не лежащие на одной прямой, проходит единственная плоскость, то через всякие две точки сферы, не являющиеся диаметрально противоположными проходит единственная диаметральная плоскость. Поэтому через всякие две точки сферы, не являющиеся диаметрально противоположными, проходит единственная большая окружность. Этот факт вполне аналогичен тому, что на плоскости через всякие две точки проходит единственная прямая. Через две диаметрально противоположные точки сферы, напротив, можно провести бесконечное множество больших окружностей. Так как всякие две диаметральные плоскости сферы пересекаются по её диаметру, то всякие две большие окружности пересекаются в двух диаметрально противоположных точках сферы. Здесь мы наблюдаем отличие сферической геометрии от плоской геометрии, в которой две прямые пересекаются не более чем в одной точке.
Так как плоскость делит пространство на две области, то большая окружность делит сферу на две области; эти области называются полусферами, а сама окружность – краем этих полусфер. Далее, так как две пересекающееся плоскости делят пространство на четыре области, то две большие окружности делят сферу на четыре области. Наконец, так как три плоскости, пересекающиеся в одной точке, делят пространство на восемь областей, то три большие окружности, не пересекающиеся в одной точке, делят сферу на восемь областей.
Полюс и поляра
Всякой большой окружности соответствует две диаметрально противоположные точки сферы, высекаемые из нее диаметром, перпендикулярным к плоскости большой окружности. Эти две точки называются полюсами большой окружности; в частности, полюсами экватора Земли являются ее географические полюсы – Северный и Южный. Очевидно, что каждым двум диаметрально противоположным точкам А и В на сфере соответствует единственная большая окружность , для которой точки А и В являются полюсами; эта большая окружность называется полярой пары диаметрально противоположных точек А и В. Каждая точка поляры называется полярно сопряженной с каждым из ее полюсов.
Еще древние греки считали окружность и сферу идеальными формами. Потверждение этому можно наблюдать в природе: многие плоды и ягоды имеют форму шара или близкую к ней, например арбуз, апельсин, смородина. Шаровидная форма используется в технике, например, в подшипниках. Во многих играх снаряд имеет форму шара: мяч в футболе, волейболе, тенесе, гольфе, шар в бильярде и др. Хорошо всем знакомый ёлочный шарик — на самом деле сфера, так как сделан из очень тонкого стекла и внутри пустой.
Форму шара имеет наша планета и большинство космических тел. А так как планеты, Солнце, Луна и звёзды движутся по воображаемой «небесной сфере», то естественно, для изучения их движения потребовалось знание геометрии сферы.
При решении задач практического характера и, в первую очередь, задач астрономии возникла сферическая геометрия. Эти задачи были необходимы, например, путешественникам и мореплавателям, которые ориентировались по звёздам.
Сведения о сфере были необходимы и при решении сугубо земных задач — вычислении географических координат, для составления географических карт, для нахождения курса корабля. В настоящее время, существуют различные науки в основе которых лежит сферическая геометрия. Например, математическая картография изучает способы отображения поверхности Земли на плоскости. Поскольку поверхность Земли (приблизительно сферическая) имеет конечную кривизну, её нельзя отобразить на плоскость с сохранением всех пространственных отношений одновременно: углов между направлениями, расстояний и площадей поверхностей. Можно сохранить только некоторые из этих соотношений. Важное понятие в математической картографии — картографическая проекция, то есть функция, задающая отображение географических координат точек на поверхности Земли на декартовы координаты на плоскости. Область картографии — составление и оформление карт.
Первой по времени геометрией, отличной от евклидовой, была сферическая геометрия, или сферика. Сферика возникла позже, чем евклидова геометрия плоскости и пространства. Основными стимулами для возникновения геометрии плоскости и пространства была необходимость измерения площадей полей и других плоских фигур и вместимости сосудов и амбаров различной формы. Основным стимулом для возникновения сферики было изучение звёздного неба.
Древние греки познакомились с вавилонской астрономией по крайней мере в IV в. до н. э., когда первоначальные названия планет были заменены названиями планет по вавилонскому образцу, латинскими переводами которых являются общепринятые нами названия. Астрономия, изложенная в «Альмагесте» Птолемея, была результатом продолжавшегося несколько веков развития науки, впитавшей традиции как вавилонских астрономов, так и греческих геометров.
Сферика Автолика. Первым античным математическим сочинением, сохранившимся до наших дней, является книга «О движущейся сфере» Автолика, жившего в конце IV в. до н. э. Предметом исследования этой книги является небесная сфера, рассматриваемая, однако, в весьма абстрактном виде. Книга Автолика состоит из 12 предложений. Определения относятся к равномерному движению. В предложении 1 доказывается, что если сфера равномерно движется вокруг оси, то все её точки, не лежащие на оси, описывают параллельные круги, имеющие те же полюсы, что и сфера, а плоскости этих кругов перпендикулярны оси сферы. Под кругами здесь понимаются плоские фигуры, ограниченные окружностями, а под выражением «точка описывает круг» понимается то, что точка пробегает окружность круга.
Сферика Феодосия. Первое дошедшее до нас систематическое изложение сферической геометрии содержится в «Сферике» Феодосия, жившего во II-I вв. до н. э. «Сферика» Феодосия состоит из трёх книг, в первой из которых шесть определений и 23 предложения, во второй – одно определение и 23 предложения, в третьей – 14 предложений. Определение Феодосия: «Сфера есть телесная фигура, содержащая внутри одной поверхности, такая, что все прямые, падающие на неё из одной точки внутри фигуры, равны между собой». Большинство предложений «Сферики» Феодосия – стереометрические теоремы и задачи на построение.
Сферика Менелая. Значительно более развитую сферическую геометрию можно найти в трактате «О сфере» Менелая, жившего в конце I в. н. э. Сочинение Менелая сохранилось только в арабском переводе в нескольких обработках, лучшими из которых являются обработки Абу Насра ибн Ирака и Насир ад-Дина ат-Туси. «Сферика Менелая состоит из трёх книг, содержащих соответственно 39, 21 и 25 предложений. Во введении к книге I Менелай даёт определение сферического треугольника («трёхсторонней фигуры»), т.е. части поверхности, ограниченной тремя дугами больших кругов, меньшими полукругами, и углов сферического треугольника. Если большинство предложений «Сферики» Феодосия были стереометрическими, сочинение Менелая посвящено геометрии на поверхности сферы, трактуемой по аналогии с планиметрией Евклида.
Сфера, большая и малая окружности
Сферой называется геометрическое место точек пространства, расположенных на данном расстоянии от данной точки, называемой её центром. Отрезок, соединяющий центр сферы с какой-либо его точкой, называется радиусом сферы. Отрезок, соединяющий де точки сферы и проходящий, кроме того, через его центр, называется диаметром. Из определения следует, что все радиусы равны и что диаметр равен удвоенному радиусу. Плоскость, проходящая через центр сферы, называется диаметральной плоскостью.
Так как через всякие три точки пространства, не лежащие на одной прямой, проходит единственная плоскость, то через всякие две точки сферы, не являющиеся диаметрально противоположными проходит единственная диаметральная плоскость. Поэтому через всякие две точки сферы, не являющиеся диаметрально противоположными, проходит единственная большая окружность. Этот факт вполне аналогичен тому, что на плоскости через всякие две точки проходит единственная прямая. Через две диаметрально противоположные точки сферы, напротив, можно провести бесконечное множество больших окружностей. Так как всякие две диаметральные плоскости сферы пересекаются по её диаметру, то всякие две большие окружности пересекаются в двух диаметрально противоположных точках сферы. Здесь мы наблюдаем отличие сферической геометрии от плоской геометрии, в которой две прямые пересекаются не более чем в одной точке.
Так как плоскость делит пространство на две области, то большая окружность делит сферу на две области; эти области называются полусферами, а сама окружность – краем этих полусфер. Далее, так как две пересекающееся плоскости делят пространство на четыре области, то две большие окружности делят сферу на четыре области. Наконец, так как три плоскости, пересекающиеся в одной точке, делят пространство на восемь областей, то три большие окружности, не пересекающиеся в одной точке, делят сферу на восемь областей.
Полюс и поляра
Всякой большой окружности соответствует две диаметрально противоположные точки сферы, высекаемые из нее диаметром, перпендикулярным к плоскости большой окружности. Эти две точки называются полюсами большой окружности; в частности, полюсами экватора Земли являются ее географические полюсы – Северный и Южный. Очевидно, что каждым двум диаметрально противоположным точкам А и В на сфере соответствует единственная большая окружность , для которой точки А и В являются полюсами; эта большая окружность называется полярой пары диаметрально противоположных точек А и В. Каждая точка поляры называется полярно сопряженной с каждым из ее полюсов.





Комментариев нет:
Отправить комментарий